Despite all appearances...

... I will not be making every entry in this blog about math.

But this one is. Feel free to skip it. I considered not even posting it, because I'm not sure anyone but me is interested in this. Forge ahead if you are. :)

The What Should You Major In? Test

Mathematics

You scored 23 mental chops, 13 work ethic, 13 bulls***ability, and 9 practicality!

So you're smart, but you're also lazy as heck and don't care too much about your post-college prospects (unless you're one of those rat race academic types or you're a dual major in something more practical). You'd make a good math major if you're really that bright--not many words, just you and the symbols, baby. That is, symbols that scare the pants off of most other people, but you've come to realize that they're a lot friendlier and easier to deal with than that pretentious literary crap. Math majors are also entitled to make the corniest jokes and pickup lines, so have at it, O awkward one. [Editor's note: Corny jokes! They read my last post!]

My test tracked 4 variables

How you compared to other people your age and gender:

You scored higher than 57% on mental chops

You scored higher than 37% on work ethic

You scored higher than 19% on bulls***ability

You scored higher than 61% on practicality

Link: The What Should You Major In? Test written by chapstiquette on OkCupid.

Well, according to an online test (and we all know how infallible those are) I at least picked the right major.

The only problem is, majoring in math seriously scares me.

Math has become increasingly abstract. Although I can do the problems and get the right answers (for the most part), there are some ideas that I simply can't seem to wrap my brain around. I have yet to figure out if the flaw lies in the way it's been presented to me, or if I have simply reached a point where I don't have the mental capacity required for complete understanding.

For example: (don't run away if this looks scary, it really isn't that bad.)

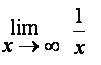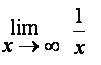This means: as x gets really really big (approaches infinity), what does 1/x approach? The bigger the number you plug in for x, the smaller the value of the fraction. If x is 4, you get 1/4. If x is 20,000,000, you get 1/20,000,000, which a lot smaller than 1/4. So, as x gets really really big, 1/x gets really really small. You can say that it is approaching zero. Make sense?

HOWEVER... when you come across this in a problem, both Calc professors I've had said to treat it as zero. But it ISN'T zero! It's really really really close, but no matter how infinitely large x becomes, 1/x still won't ever actually equal zero. The way I see it, if you call that zero, you don't get an exact answer. You get one that's REALLY REALLY close. But we call it exact. Does that seem like flawed logic to anyone else?

I think I just need an amazing professor who will take the time to explain it to me.

I hope that's the solution, anyway.

Or maybe I should be a liberal arts major and teach 4th grade instead of high school. That way I can teach fractions. Most of the students I tutor who are having a hard time in algebra are terrible at fractions. Coincidence? No.

That's a whole 'nother problem in itself. My original plan when I started community college was to teach elementary school. So I took Math For Elementary Teachers. It was absolutely horrifying to me how many people in that class were terrible at math. This was not the difficult stuff folks, we're talking fractions and decimals here. Not even algebra. The test scores were astonishing. And these people want to TEACH ELEMENTARY SCHOOL! If someone barely passed Math for Elementary Teachers with a C-, do you want them teaching YOUR kids the basic math skills they need to be successful in Algebra? I certainly don't.

I suppose I could write a much longer rant about this, but I think I'd better get myself more thoroughly educated on theories about teaching/training teachers before I form a solid opinion on What's Wrong With Education In the United States.