Ouch.

I attend school at Pepperdine University, which is notorious for its many stairs. Seriously, Google "Pepperdine stairs", you'll see. Just as my campus is known for its stairs, so have I made a name for myself by falling down them. At least once a semester. Thankfully, I have mastered the art of falling backward and bracing myself to avoid a full head-on tumbling down. My tailbone is perhaps not as thankful for this technique as my head. I thought I was going to avoid it this spring, but a little tiny staircase of four caught me off guard. My foot slipped out from under me, and down I went. Since my school is also known for its extremely friendly and caring student body, a few people stopped to see if I was okay, and not one of them giggled at all. I shrugged it off and got up, but now... ouch. My whole left side just feels out of whack.

I've been pondering this all day. I am kind of clumsy. I run into things a lot. People say ouch on my behalf far more often than I do, because I bang my various extremities into walls on such a regular basis that I barely notice it anymore. I have pretty constant bruises on my shins. Plus the whole not-good-with-stairs thing. My husband actually makes it a point to walk in front of me when we go down stairs together, just in case I start to fall. He's big, he'll catch me (or at least that's the theory.) But why am I clumsy? Other people don't fall down stairs twice a year! I took dance from ages 4 through 17, aren't I supposed to be graceful? I have terrible vision, and although I wear contacts to correct it, I sometimes wonder if that isn't somehow a cause of my klutzitude. Or maybe I'm just fishing for excuses here.

I wonder if God might have compensated me for this in some way I have yet to discover: "Michelle will always have greeny-purple elbows, but she makes a mean pot roast" or something along those lines. I'll be sure to update if I figure that one out.

(3/8/07 ETA:
I went ice skating for about two hours on Saturday. I didn't fall once, and I began to think that I might not be as clumsy as I previously thought. Half an hour later, my humility was restored when I had the audacity to step off a curb. I like to think I was just decorating my knees for Easter. If eggs get to be pretty pastel colors, why not my legs?)

Soulmates

For those who don't speak math, this says: For all x in P, there exists a unique y in P, such that x plus y equals love, where P is the set of all people. In other words, everyone has a soulmate.

Forget French and Italian, I say Math is the true romance language. And people from every culture speak it.

Quirks

As I have shared earlier, I count stairs. If I'm not having a conversation with someone and I'm going up or down stairs, it's safe to bet that I'm (silently, thank goodness) counting them as I go. I know another math person that does this too. Also, due to twelve years of dance classes, I occasionally start counting them in eight-counts.

When looking at a digital clock, I often attempt to make true mathematical statements out of the time, i.e. 6:23 is 6=2x3. This started when I was about six years old on a cross country car trip to Illinois. My favorite ones to catch involve square roots. 7:49, yay!

If I'm eating something that comes in individual pieces (like M&M's), I want to chew the same number of pieces on each side of my mouth. So I alternate.

If I step on a crunchy leaf with one foot (which I usually do on purpose, crunching leaves is nice!), I feel funny if I don't also step on a crunchy leaf with the other foot.

In written language, nothing bothers me more than when "less" is used where "fewer" should be. It happens all. the. time. For the record, "fewer" is used if the object of the adjective can be counted. There is less milk in the glass, but there are fewer glasses of milk. (Bold, italic AND large size font, just to emphasize how much I hate that mistake.)

When I play computer solitaire, I line up the cards at the end like this, so that I can put four cards of the same suit in the correct pile in order. I told my husband this, and now when he wins, he lines them up like this and lets me finish.

My spider solitaire quirk is worse. When the cards pile up in the bottom left corner, they have to be in some kind of pattern (black-red-black-red, or black-red-red-black, you get the idea.) If the game goes in such a way that the pattern is messed up, it's entirely possible that I will quit and start a new game.

I'm sure there are more, but quite frankly, I don't want to lose any friends. People can only put up with so much.

Mnemonic fun!

Finals are over, and not a moment too soon. My worst one was for Real Analysis, a proof-intensive math course where we essentially proved that calculus works. (See My Infinity Is Bigger Than Yours for more fun from this class, which, by the way, is a nice spread out TWO SEMESTER COURSE at most schools... but not mine.) I spent most of Saturday studying for this final, a lot of which was getting the specific definitions straight for the main concepts (makes proofs a lot easier when you can quickly and clearly define everything you're talking about). You know what I realized? Most of the important concepts from this class start with the same two letters. Compact, complete, connected, convergent, continuous... I think it's a conspiracy aimed at those of us who remember things better when we can make an acronym out of them.

So this is what my brain did to compensate for the lack of acronymage. (<--Whee! New words!) When I took a break from studying to shower and my eyes landed on my bottle of Olay Complete body wash, my first thought was "Every Cauchy sequence in that bottle of body wash converges to a point also in that bottle!" which I know makes zero sense to non-math-people, but that's the definition of complete.The ease with which my brain made that connection actually irritated me for a second, because I would like to be able to pretend that I think like a normal person. (I know this isn't true, because I also do weird things like count stairs as I go up and down them. I've found other math people who do this too. But I digress.) Once I was finished being irritated, I realized that this was an excellent way to keep all those definitions straight. I went on to picture compact cars with covers that had finite subcovers, and connected trains where the only cars with doors that were both open and closed were the cars that contained everything in the train and the cars that contained nothing.

I'm kind of embarrassed by this.

And at the same time, kind of proud.

Kind of.

It's probably a good thing that I have a three week break for Christmas now.

Technology in the classroom

Last week, in my Education and Society class, we had a fascinating discussion about the use of technology in the classroom. Precious little research has been done on whether it actually aids learning, but many districts will pour money into it without a second thought, because technology=good. Much of the time it can be more of a distraction than an aid: spending 15 minutes of class time trying to get the overhead projector to work is not increasing active learning time. Not to mention the technology that isn't intended for use in the classroom. High school students are notorious for texting or taking calls during class. I'm sure there's a much longer post about this inside me somewhere, but what I'm getting at is this:

During this wonderful, informative and engaging discussion, my cell phone rang.

I am, apparently, part of the problem.

Reason #283,701 why I want to be a math teacher

I got my hair cut last week. As I was waiting in line to pay for the cut and some shampoo, the power went out. No problem for me, I was paying cash. Following is the sequence of events that occured as I stepped up to the register.

1) Cashier 1 writes up an invoice by hand that doesn't include tax on the shampoo, gives me the total.
2) Cashier 2 catches her mistake, but doesn't know what the sales tax rate is. Goes in the back to check.
3) Cashier 2 returns, and they huddle over the calculator together. Cashier 2 enters: $13.00 x 8.25. Yielding a sales tax of $107.25. Cashier 1: "That can't be right." I breathe a sigh of relief, because I wasn't carrying quite enough cash to cover an 825% sales tax rate.
4) Cashiers 1&2 stare at calculator.
5) I pipe up: "Enter thirteen times point-zero-eight-two-five." They look at me incredulously. "Trust me."
6) Cashier 2 enters 13 x zero-point-eight-two-five, yielding a sales tax of $10.725. She gives a befuddled little laugh that seems to say, "Where did my education go wrong?" Or maybe that's just how I interpreted it. Me: "thirteen times POINT-zero-eight-two-five".
7) Cashier 2 enters it correctly, yielding the much-more-budget-friendly sales tax amount of $1.0725. I'm glad they've got it, but wonder how they'll fare with the customers in back of me.
8) I restrain the urge to return the next day, math book in hand, and introduce these ladies to the lovely world of percentages. Instead, I file this story in the back of my head, to retrieve when my future students ask me, "But when are we ever going to USE this?" Every day folks, every single day.

Eavesdropping

This morning, I finished my 8am class and had a little less than an hour to read a chapter for a quiz in my education class. I went to the lobby of the building to read instead of the library like I usually do, mostly because I have a terrible cold and didn't feel like making the extra effort to walk over there. I began to read, and just could not concentrate, thanks to three girls having a conversation across the room. Normally, I'm pretty adept at tuning people out when I read. I can study just about anywhere without a problem, but this morning, it was impossible. Naturally, since I couldn't tune them out, I was listening to what they were saying. The first phrase I caught was "relationship with him", which had me a little annoyed that they chose MY reading spot to have a conversation about guys. Then I realized, they weren't talking about boys, they were talking about their relationships with God.

Most of the conversation was about school, and how they stress themselves out over trying to be perfect students (something I can relate to). They talked about how when they just stop trying to control that part of their lives and trust God to take care of it, He does. When they make time to spend with Him even though they "should be" writing a paper or studying for a class, the deadline for the paper gets pushed back and classes get canceled. Trust things to God and he will take care of them for you. They had a lot more to say about it, but that was the general idea, and they closed with a warm, heartfelt prayer.

When they finished, I got their attention and admitted that I had been eavesdropping. I told them that I was having a hard time tuning them out, but that their converstation had been exactly what I needed to hear. They were happy to hear it, made enthusiastic, friendly introductions, invited me to join them next week and told me they would be praying for me and my quiz. We said goodbye and I turned back to my work.

After all this, I had about twenty minutes to do the reading, which was basically enough time to read the chapter summary and hope for the best. At that point I had pretty much decided that doing poorly on this one quiz was a fair price to pay for the uplifting discussion I got to be a part of. I finished up the summary and went to class.

Quizzes in this class are 7 or 8 questions that we each sit and take individually: a couple true-false, some multiple choice, and a short answer or two. We've had lots of quizzes since the beginning of the semester, and they've all been basically the same. Today? Group quiz. We've never had a group quiz before, we probably won't again, but today we had one, just when I needed it most. Yet another example of how God knows what we need, and provides it for us.

1+1=2

OFFICIAL NOTICE: Until otherwise notified, please assume that this blog IS devoted entirely to math. Because I apparently never have anything interesting to say about anything else.

More about the introductory proof-writing class. We've spent the last couple days proving things that, up until this point, we simply accepted as true. Like this: If a>b, then a+c>b+c. Meaning you can add something to both sides of an inequality and the inequality is still true (for example: since 2>1, 2+3>1+3.) Obvious, right? Most of us probably used this kind of thing back in middle school, if not earlier. But actually writing a formal proof is not quite the same thing. Of course we can all SEE that the statement is true, but why it's true (and the steps to get there) are more important. It requires a different style of thinking than other math we've done up to this point, although once you get the idea it's actually kinda fun. So anyway, after a few days of proving stuff we always thought we knew, our professor writes this on the board:

1+1=2

And asks, "Why?"


You have never heard a more silent room.


Please note, this is a room full of math majors.



Thinking about it still makes me giggle.


After about 10 seconds, people started throwing out ideas, none of which were particularly correct. But at least we were trying.

It turns out it's true by definition. 2 is defined to be the sum of 1 and 1. Which was awfully nice, because none of the assumptions or theorems we had to work with were getting us anywhere close.

I love this class.

I lied.

Although I said every post in this blog wasn't going to be about math, I'm three for three here. I may have doomed myself from the beginning with the title. Stick with me, and I'll try to have something else on my mind someday.

I'm taking Transition to Abstract Mathematics, which is neither as frightening nor as impressive as it may sound. It's about writing proofs, and before we get to actual proof writing (which I should be working on now, but that's beside the point), we've learned some basic logic. Lots of if-then statements, with some ands, ors, existential and universal quantifiers thrown in for good measure. We've been playing around with these a lot in preparation for some simple proofs.

The point: As I left class on Friday (my last class, the last day of the week), I realized I was pretty tired, and though it might be a good idea to get something caffineated for my (hour-and-then-some) drive home. The thought that popped into my head?

"If it's hot in my car, then I'll go to Starbucks and get an iced Chai tea latte."

I then proved to myself I've been spending too much time in that class.

This is logically equivalent to "Either NOT the first thing, or the second thing". Meaning, either it's not hot on my car, or I go to Starbucks and get an iced Chai tea latte.

Converse: "If I go to Starbucks and get an iced Chai, then it is hot in my car." (Not logically equivalent to the first statement... I could go to Starbucks for an iced chai even if my car was a cooler temperature.)

Inverse: "If it's not hot in my car, then I won't go to Starbucks and get an iced Chai."
(Also not logically equivalent to the first, for the same reasons above.)

Contrapositive: "I don't go to Starbucks and get an iced Chai, so it isn't hot in my car." (A-ha. This one IS logically equivalent!)

All this nonsense occured to me on the walk from my class to my car, at which point I decided that this train of thought was evidence that was certainly in need of both an iced Chai (veinte, in case you were wondering) and a relaxing weekend. After both, I think I'm ready to go tackle my homework. Because: IF I don't do the homework, THEN I won't understand what's going on in class tomorrow.

Despite all appearances...

... I will not be making every entry in this blog about math.

But this one is. Feel free to skip it. I considered not even posting it, because I'm not sure anyone but me is interested in this. Forge ahead if you are. :)

The What Should You Major In? Test

Mathematics

You scored 23 mental chops, 13 work ethic, 13 bulls***ability, and 9 practicality!

So you're smart, but you're also lazy as heck and don't care too much about your post-college prospects (unless you're one of those rat race academic types or you're a dual major in something more practical). You'd make a good math major if you're really that bright--not many words, just you and the symbols, baby. That is, symbols that scare the pants off of most other people, but you've come to realize that they're a lot friendlier and easier to deal with than that pretentious literary crap. Math majors are also entitled to make the corniest jokes and pickup lines, so have at it, O awkward one. [Editor's note: Corny jokes! They read my last post!]

My test tracked 4 variables

How you compared to other people your age and gender:

You scored higher than 57% on mental chops

You scored higher than 37% on work ethic

You scored higher than 19% on bulls***ability

You scored higher than 61% on practicality

Link: The What Should You Major In? Test written by chapstiquette on OkCupid.

Well, according to an online test (and we all know how infallible those are) I at least picked the right major.

The only problem is, majoring in math seriously scares me.

Math has become increasingly abstract. Although I can do the problems and get the right answers (for the most part), there are some ideas that I simply can't seem to wrap my brain around. I have yet to figure out if the flaw lies in the way it's been presented to me, or if I have simply reached a point where I don't have the mental capacity required for complete understanding.

For example: (don't run away if this looks scary, it really isn't that bad.)

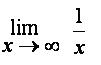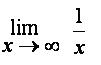This means: as x gets really really big (approaches infinity), what does 1/x approach? The bigger the number you plug in for x, the smaller the value of the fraction. If x is 4, you get 1/4. If x is 20,000,000, you get 1/20,000,000, which a lot smaller than 1/4. So, as x gets really really big, 1/x gets really really small. You can say that it is approaching zero. Make sense?

HOWEVER... when you come across this in a problem, both Calc professors I've had said to treat it as zero. But it ISN'T zero! It's really really really close, but no matter how infinitely large x becomes, 1/x still won't ever actually equal zero. The way I see it, if you call that zero, you don't get an exact answer. You get one that's REALLY REALLY close. But we call it exact. Does that seem like flawed logic to anyone else?

I think I just need an amazing professor who will take the time to explain it to me.

I hope that's the solution, anyway.

Or maybe I should be a liberal arts major and teach 4th grade instead of high school. That way I can teach fractions. Most of the students I tutor who are having a hard time in algebra are terrible at fractions. Coincidence? No.

That's a whole 'nother problem in itself. My original plan when I started community college was to teach elementary school. So I took Math For Elementary Teachers. It was absolutely horrifying to me how many people in that class were terrible at math. This was not the difficult stuff folks, we're talking fractions and decimals here. Not even algebra. The test scores were astonishing. And these people want to TEACH ELEMENTARY SCHOOL! If someone barely passed Math for Elementary Teachers with a C-, do you want them teaching YOUR kids the basic math skills they need to be successful in Algebra? I certainly don't.

I suppose I could write a much longer rant about this, but I think I'd better get myself more thoroughly educated on theories about teaching/training teachers before I form a solid opinion on What's Wrong With Education In the United States.

A short explanation.

The name of this blog proves, without a doubt, that I have crossed some kind of line.

On one side of this line, there are those who are simply "good at math".

On the other side is my Math 104 professor who not only looked but also sounded just like Elmer Fudd. He enjoyed jokes like this one:

What transformation is this?

(Long pause while all of us math/engineering/etc. majors rack our brains, thinking we MUST have learned this somewhere along the line.)



...
...
...




The parting of the Red Sea!

Of course, since he had that unfortunate speech impediment, it came across as "The pawting of the Wed Sea!" He tried to tell it to us three times in the course of a semester.

I've joined him.

I was searching for something a little more clever than "Michelle's Blog" for a title. In my search, I came across this:

Jesus and his disciples were walking around one day, when Jesus said, "The Kingdom of Heaven is like 3x squared plus 8x minus 9." The disciples looked very puzzled, and finally asked Peter, "What on earth does Jesus mean - the Kingdom of Heaven is like 3x squared plus 8x minus 9? Peter said, "Don't worry. It's just another one of his parabolas."

Did you laugh out loud at that?

Because I did.

I have definitely crossed some kind of line. So it begins.